翻轉數學從布題開始~以四年級概數為例

國小數學屬於生活數學，與國中的純數學習有很大的不同，

顧名思義就是從生活中的例子來讓孩子們察覺到數學與生活的關係，

然後理解數學是如何存在於生活周遭，

接下來當然就是藉由老師的教學來讓孩子們懂得如何應用數學來解決生活中的問題。

因此，

數學課堂上，老師的布題內容就會扮演關鍵性的角色，

決定著孩子們會從生活出發來學習數學，

還是循著成人算則的模式來學習數學!

現在的課本教材編排已經有不少的進步，

以康軒四下課本內容為例: (按下圖檔可放大)

題目中並未指明要用哪一種方法來取概數，

然後布題內容也符合生活經驗，

孩子們就算不懂概數，

也能用除法來算出答案!

問題是，

概數的學習應該不能引導孩子們使用除法來解題吧?

當然啊!

課本也沒有要孩子這樣做，

問題是光看題目本身，

你認為孩子們知道要用概數來思考嗎?

而且一旦孩子們拿著課本上課，

而課本寫得這麼詳細，

我想孩子們也不用努力思考了吧!

這也就是為什麼我上課幾乎不太用數學課本的原因。

所以，

如果布題改成

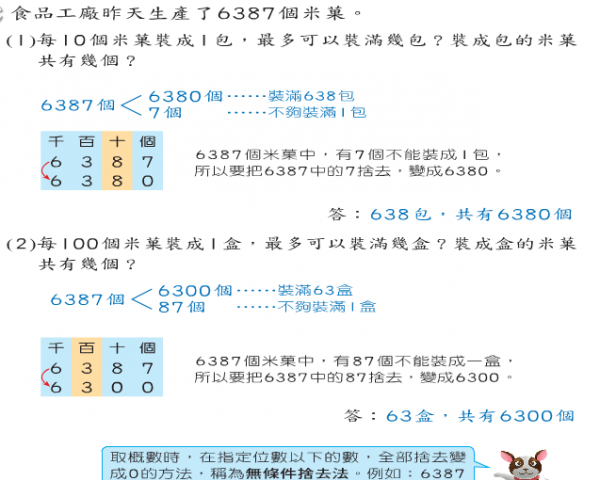
"食品工廠昨天生產了6387個米菓。

每10個米菓裝成一包，最多可以裝滿幾包?裝承包的米菓共有幾個?

有辦法不用計算，就能看出答案嗎?"

試想，

這樣的布題會不會更符合學習的需求呢?

孩子解題時，

口語表達可能會這麼說:

"因為每10個米菓裝一包，問最多裝滿幾包，

表示一包一定要10個，

因此6387有638個十，

所以是638包，

而638個十也就是6380個米菓。

然後再經驗幾題類似的情境題後，

孩子們因為題目上的需求而都採用了相同的策略，

那麼此時宣告"無條件捨去法"的定義，

然後再回到情境題去看題意，

理解到

6387 -> 6380 這樣就稱為"使用無條件捨去法取概數到十位"，

是不是更能促進孩子們理解概數在生活上的運用，並習得在數學上相對應的概念呢?

在孩子們依照這樣的流程，

習得無條件捨去與無條件進入法之後，

當然，

四捨五入就要上場了!

問題是，

如何讓四捨五入法"上場"上的自然，也就是能激發孩子們解題的需求呢?

再來看看課本吧!

如果將布題僅呈現如下的資訊，

情況會有不一樣嗎?

我認為是會有的，

而且會有很大的不一樣。

如果在前面的教學中，

孩子們理解概數是大約的數，

但不可和正確的數誤差太大，

不然概數就沒有存在的意義了。

那麼，孩子們的舊經驗是只知道無條件進入與捨去法，

所以忠孝國小的2267人會以無條件捨去取千位

2267->2000 , 因為這樣和原數值才不會誤差太大。

那仁愛國小的2875人就會以無條件進入取千位，

2875 -> 3000

當討論到了信義國小的3472，以及和平國小的2500，

孩子們就會發生疑問，對誤差的選擇開始爭論該是無條件進入或無條件捨去，

甚至會出現兩種取概數法都可以的論點，

這時宣告四捨五入法的時機就到了!

其實，

四捨五入法是不能被推論的，

因為這是屬於社會數學知識，也就是一種共同的數學約定。

看到這裡，

希望可以讓大家理解題目內容的選擇真的非常重要，

雖然沒有一定的公式可循，

但要能刺激孩子們思考，且不誤導思考方向的題目，

可是要請大家再布數學題目前多思量一下喔!