「雙曲線」課程講解與教學實作-數學咖啡館

「雙曲線」課程講解與教學實作-數學咖啡館
photo creditflickr@ Andrew Gustar ,by-nd 2.0
雙曲線課程講解
●115-117 雙曲線基本定義 https://youtu.be/5T_8FQbMyYk
●118-125 雙曲線諸元 https://youtu.be/BMbWNzpegmI
●126-129 雙曲線其他諸元與性質 https://youtu.be/pGBTWLis1sA
●130-131 雙曲線定義例題 https://youtu.be/siRO9fEAUUE
●132-134 定義型學測題 https://youtu.be/UKwjTDSrBI8
●135-137 判斷雙曲圖形(學測題) https://youtu.be/-rd_8imuQLA
●138 雙曲線的切線折痕與作圖 https://youtu.be/EsFT4IXirL4
●139 例10:雙曲之切線(折痕)應用 https://youtu.be/vABXM-rMn1g
●140 例11:圖形判別與交點、101學測 https://youtu.be/fHbJj41sm4g
●141 例12:圖形判別與交點、102學測 https://youtu.be/pV06KX5UMcg
●142-148 焦半徑定義 https://youtu.be/BfjhnjIMh3E
●149-154 漸近線說明與作圖 https://youtu.be/4pcc1V8T5YQ
●155-158 漸進線例題 https://youtu.be/Ls4DwIf0tyU
●159-166 漸近線性質 https://youtu.be/L4a1PzWyfNQ
●167-169 共軛雙曲線 https://youtu.be/7OEXjoyMdOc
●170-178 等軸雙曲線 https://youtu.be/h3opURP8kiM
●179-183 共焦點問題 https://youtu.be/6VYzwyA-m5s
●184-187 雙曲線的伸縮 https://youtu.be/XYssUywWkYw
●189-191 雙曲線參數式 https://youtu.be/8bYZqtf0Htk
●191-194 動點軌跡 https://youtu.be/dAwiWTInK4w
●雙曲心智圖 https://youtu.be/Fe-MFvuuz4c
分享孩子們共思出兩類收斂圖:
第一層核心觀念繞著-「焦半徑差=貫軸長」定義,導出標準式與諸元。
第二層觀念-「漸近線」的定義,再重新詮釋雙曲線,今年的104學測就提及這方面的概念。
第三層為應用,大多圍繞第三冊所學,三角函數、直線、坐標、面積等觀念。
高中雙曲線章節,切忌東背西背一堆公式、題型,請細心判讀完題目,即可作圖解決之。
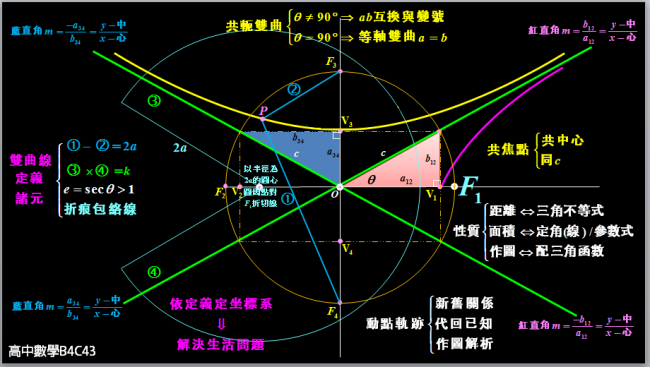
圖像式心智圖
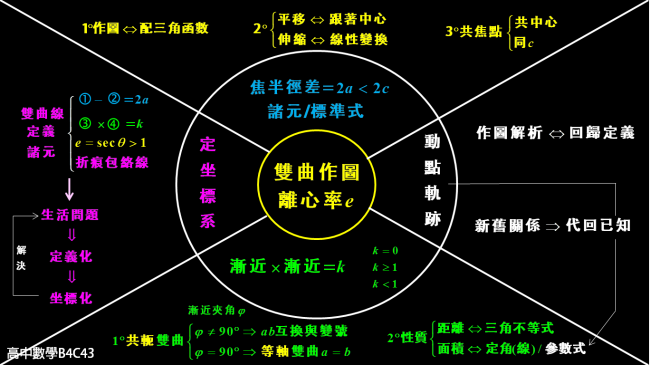
文字型心智圖
數學咖啡館實作流程:
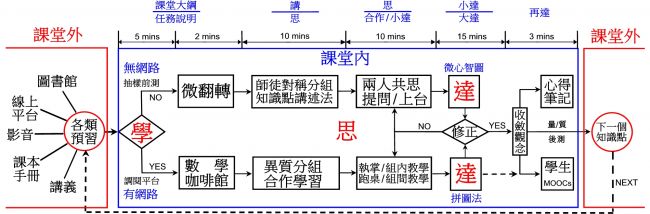
數學咖啡館-組內共思微翻:
因為期末將至,這章節沒有實施大翻轉式的拼圖法(Jigsaw III),
採用微翻師徒模式授課,小觀念收斂於心得筆記中(小心智圖),
只選取一組課堂樣本分享,其餘俟考後再行補充。
在此也特別感謝均一的曲智鑛老師,
來觀來議這節雙曲折痕課,給予諸多寶貴的建議。

雙曲線折痕(學生作品)

學生雙曲線微心智圖(未拼圖)
數學咖啡館-互助共享共好共備
您的思考不只是直直的一條線,
您需要的是能轉彎、能伸縮、能旋轉的思考維度,
您有時更需要朋友來一起討論、解決問題,這樣才能編織成更高維度的思考,
您將會事半功倍,當收穫愈來愈多,甜頭將成為數學共享共備的動力,
您的能階,當互助共好充滿能量後,將躍升到另一層次,
您若能飛龍在天,再往下反思任何問題,
都只是在陳述自然界中剛好如此完美的定理,同時也證明、成就您的存在!
唯有飛得更高,方能看得更遠,遠離塵囂瑣碎之事。共勉之~
敬祝老師們教安,同學們期末順心順利。
您可能有興趣






